[Anomaly Detection] SVM, SVDD

# One-Class Support Vector Machine (One SVM)

- 정상 / 불량 관측치를 부분짓는 서포트 벡터 머신 알고리즘을 구축하는 방법론

- 정상 데이터를 고차원 공간으로 보내서 ①불량 데이터와 구분되고 ②원점에서 멀리 떨어지게 하는게 목표

w: parameter regularization으로 특정 범위에서만 변하게 함 (민감하게 변하지 않게; Robust)

ρ: 원점으로부터의 거리. 멀면 좋은데 목적식을 최소화해야 하므로 -를 붙임. 

ν: nu라고 읽음. SVM의 C를 (1/νn)으로 표현. 

ξ: hyperplane과 원점 사이에 있는 점들의 hyperplane까지의 거리. (최소화)

Φ(.): mapping function (original data → feature space)

 

# 최적화

SVM과 마찬가지로 제약식을 목적식으로 올려주기 위해 Lagrangian primal 형태로 바꿔줌. 

α, β는 Lagrangian parameter

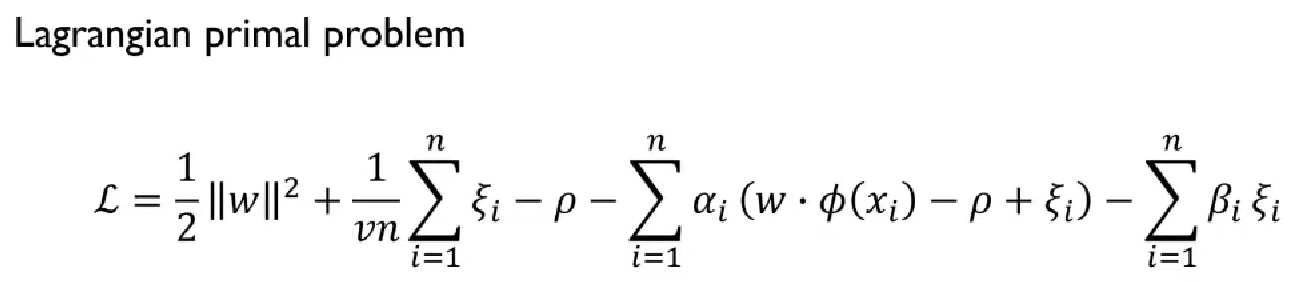
w, ξ, ρ 각각에 대해 미분

w를 대입해서 α에 대한 식으로 정리하면 정리 가능한데 일단 패스 (이해안됨 ㅎㅎ)

 

정리하면 이렇게 됨. 

# 해석

정상 관측치를 "안"으로 표현했을 때,

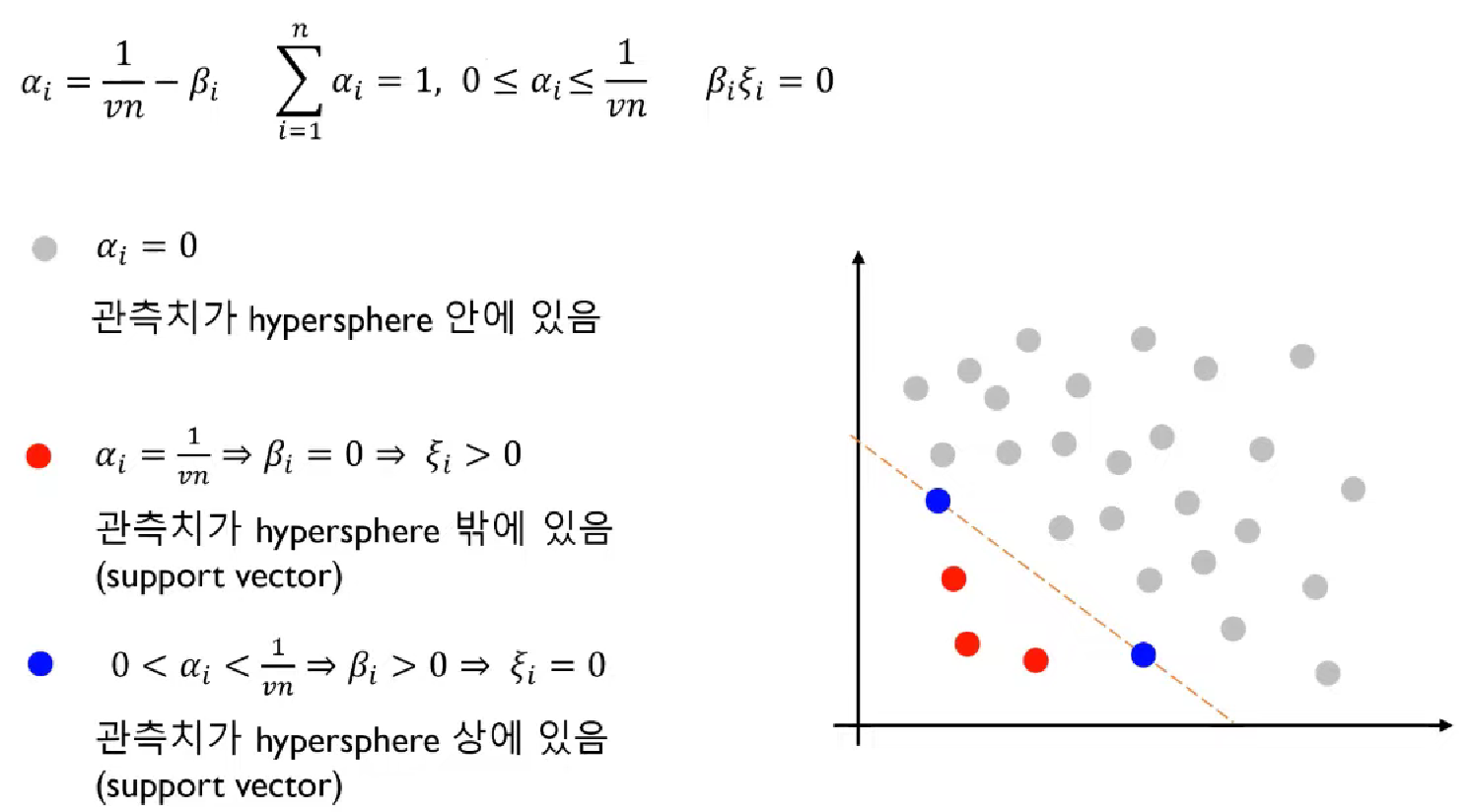
# ν (nu)

- 0 ≤ ν ≤ 1

- 최소 νn개의 support vector가 존재. n은 바꿀 수 없으므로 ν를 조절해서 support vector 수를 조절

- 예: n=5000, ν=0.1

        > 5000개의 전체 정상데이터에서 적어도 500개 이상의 support vector 존재

        > 이 중 패널티가 부여되는 support vector는 최대 500개

- 결론적으로 ν를 조정해서 경계를 정한다. (작을수록 전체가 포함)

 

솔직히 잘 모르겠다. 다음에 다시 보자. 

# SVDD 

- Support Vector Data Description

- 데이터를 feature space로 trainsform하여 mapping

- 정상 관측치를 감싸는 가장 작은 hypersphere 구축 (중심 a, 반지름 R)

구 내부면 정상, 바깥이면 비정상으로 간주

- ξ(크사이)를 최소화해야하지만, 구가 너무 크면 overfitting

# Formulation

목적식: 정상데이터를 최대한 컴팩트하게 아우르는 구를 찾기

             단, 에러를 허용함

제약식: feature space의 점(Φ)과 중심(a)과의 거리 반지름(R)보다 작아야 한다. (단 에러는 허용; ξ)

 

# 최적화

푸는 방식은 역시 Lagrangian primal problem 형태로 푼다. 

 

똑같이 미지수에 대해 미분해서 대입한다. (a, R, ξ)

마찬가지로 대입하고 kernel function 어쩌고저쩌고 풀면 결국은.. 솔직히 잘 모르겠으니 나중에 또 보자. 

# 해석

C가 크다 →  ξ를 허용하지 않음 → 밖에 나가는 데이터를 허용하지 않음 (다 포함하려 함) 

sigma가 작음 → 분산이 작음 → overfitting

 

참고: https://youtu.be/CjvMZmMTmQc