랜덤포레스트 (Random Forest)

# 개요

개별 트리 모델은 아래와 같은 단점을 가지고 있다. 

• 계층적 구조로 인해 중간에 에러가 발생하면 계속 전파됨
• 학습 데이터의 미세한 변동에도 영향을 크게 받음
• 노이즈에 영향을 크게 받음
• 최종 노드의 수를 너무 늘리면 과적합 위험

이를 해결하기 위한 모델이 랜덤 포레스트이다. 

 

# 앙상블

여러 Base 모델의 예측을 다수결이나 평균을 이용해 통합하여 예측 정확성을 높이는 방법

 

다음 조건을 만족하면 앙상블 모델은 Base 모델보다 우수한 성능을 보여준다. 

• Base 모델들이 서로 독립적
• Base 모델들이 무작위 예측보다 성능이 좋은 경우 

앙상블 모델의 오류율은 아래와 같이 나타난다. 

예시로 5개의 binary classifier를 base 모델로 앙상블하면 오류율은 아래와 같다. 

어떤 모델을 base 모델로 사용하냐에 따라서 앙상블 결과가 달라진다. 

 

랜덤 포레스트는 의사결정나무 모델을 base 모델로 사용한 것이다. 

이는 아래와 같은 장점을 가진다. 

• Low computational complexity : 데이터의 크기가 방대한 경우에도 모델을 빨리 구축할 수 있다. 
• Nonparametric : 데이터 분포에 대한 전제가 필요하지 않다. 

 

# 랜덤 포레스트

다수의 Decision tree에 의한 예측을 종합하는 앙상블 방법

 

하나의 Decision tree보다 높은 예측 정확도를 보인다. 

 

관측치의 수에 비해 변수가 많은 고차원 데이터에서 feature selection 기법으로 널리 사용된다. 

 

진행은 크게 세 단계로 분류된다. 

1. Bootstrap 기법을 이용하여 다수의 training data 생성
2. 생성된 training data로 decision tree 모델 구축 (무작위 변수 사용)
3. 예측 종합

핵심 아이디어는 diversity, random을 확보하는 것으로 아래 두 가지가 중요하다. 

1. Bagging : 여러 개의 Training data를 생성하여 각 데이터마다 개별 Decision tree 구축
2. Random subspace : Decision tree 구축 시 변수 무작위로 선택

 

# Bagging (Bootstrap Aggregating)

샘플링 기법으로 다음 두 가지가 중요하다.

1. 복원추출
2. 원래 데이터의 수 만큼 샘플링

## Bootstrap

아래 그림처럼 원래 데이터의 수 만큼 뽑아야 한다. 

이론적으로 한 개체가 하나의 부트스트랩에 한 번도 선택되지 않을 확률은 아래와 같다. 

## Aggregation

그리고 결과를 Aggregation 해야 하는데 여러가지 방법이 있다. 

Majority Voting

다수를 선택하는 방법으로 아래와 같이 표현할 수 있다. 

식이 어려워보이지만 1과 0 각각을 카운트해서 더 큰쪽의 클래스의 값을 따르는 것이다. (argmax)

 

Weighted Voting 1

각 모델의 accuracy를 고려하여 가중평균을 하는 방법이다. 

 

식은 아래와 같은데 1, 0대신 모델의 accuracy를 사용하는 것만 다르다. 

Weighted Voting 2

각 클래스에 대한 확률을 고려하여 구하는 예측하는 방식이다. 

 

식은 비슷한데 각 클래스에 대한 숫자로 나누는 것이 아니라 전체 크기인 n으로 나누는 것에 주의하자. 

# Random subspace

하나의 Decision tree에서는 모든 변수를 고려하여 최적의 변수를 선택해서 분기했다. 

 

랜덤포레스트에서는 Decision tree의 분기점을 탐색할 때

 

원래 변수의 수 보다 적은 수의 변수를 임의로 선택한다. 

 

# Generalization Error

랜덤포레스트는 트리의 수가 충분히 많으면,

 

Strong Law of Large Numbers에 의해 과적합 되지 않고 에러가 특정 값에 수렴한다. 

 

아래 식은 error의 Upper bound를 나타낸 것으로 작을 수록 좋다. 

ρ : Decision tree 사이의 평균 상관관계

s : 올바르게 예측한 tree와 잘못 예측한 tree 수 차이의 평균

 

개별 tree의 정확도가 높을 수록 s가 증가한다. 

 

Bagging과 random subspace 기법은 각 모델의 독립성, 일반화, 무작위성을 통해 ρ를 감소시킨다. 

 

# Feature Importance

선형 회귀나 로지스틱 회귀에서는 각 변수가 얼마나 유의미한지 알 수 있다. 

 

그러나 랜덤 포레스트에서는 그런 정보는 없다. 

 

대신 간접적으로 Feature Importance를 구할 수 있다. 

 

## Out of bag (OOB)

Feature Importance를 알기 전에 OOB를 알아야 한다. 

 

Bagging의 경우 모든 데이터를 사용하는게 아니다. 

 

여기서 부트스트랩에 포함되지 않은 데이터를 Out of bag이라고 한다. 

 

이를 검증에 사용할 수 있다. 

 

## Importance 계산

(1) 각 부트스트랩에서 생성된 Tree에 대한 OOB error를 구한다. (r)

 

(2) 특정 변수 Xi의 값을 임의로 뒤섞고 다시 OOB error를 구한다. (e)

 

(3) 1번과 2번에서 구한 값의 차이를 구한다. 

(4) 3번에서 구한 에러를 분산을 고려하여 스케일링한다. 

d가 크다는건 그 변수가 뒤바꼈을 때 영향이 크다는 뜻이므로 중요도가 크다. 

 

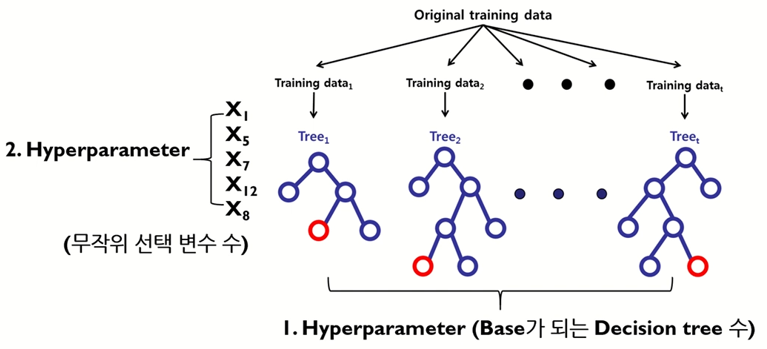
# 하이퍼 파라미터

1. Decision tree의 수

이론상 Strong law of large numbers를 만족시키려면 2천개 이상의 decision tree가 필요하다. 

실제로는 더 적은 수로 되는 경우도 많이 있다. 

 

2. Decision tree에서 노드 분할 시 무작위로 선택되는 변수의 수

이론상은 classification의 경우 root(변수의 수), Regression은 (변수의 수) / 3 을 추천한다. 

 

 

랜덤포레스트로 Regression을 할 경우는 평균을 취하면 된다. 

 

 

참고 : 김성범 교수님 유튜브