Decision tree

# 개요

데이터에 내재된 패턴을 변수의 조합으로 나타내는 예측/분류 모델을 '나무의 형태'로 만드는 것을 뜻한다. 

 

질문을 던져서 맞고 틀리고에 따라 대상을 좁혀가는 방식으로 스무고개 놀이와 비슷하다. 

 

데이터가 균일하도록 분할해야 하는데 분류냐 예측이냐에 따라 분할하는 방식이 다르다. 

 

하나의 특징으로는 Terminal node의 값을 모두 더하면 Root node의 값과 같다. 

 

# 이진분할

위에서 본 트리 형태는 사실 아래와 같이 표현할 수도 있다. 

 

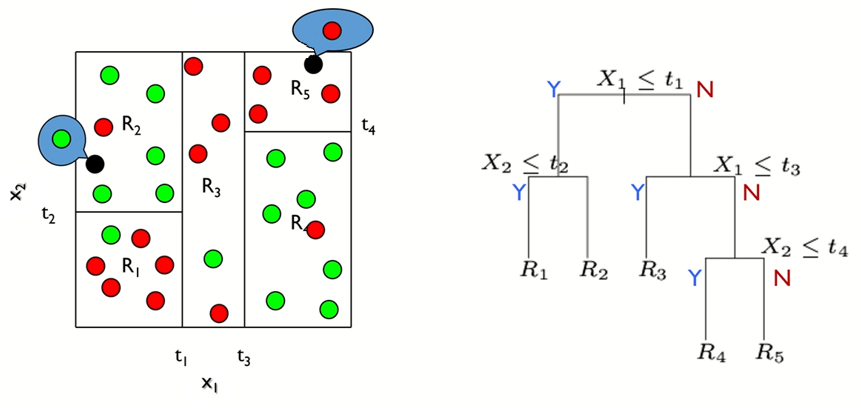
왼쪽은 변수가 2개일 때,  가운데는 변수가 3개일 때를 뜻한다.

 

이런 표현법도 장점이 있긴 하지만 변수 4개 부터는 표현이 어려워서 보통  오른쪽 방법으로 표현한다. 

 

# 예측나무 모델 (Regression Tree)

x₁, x₂ 두 개의 변수로 이루어진 데이터의 경우 아래와 같이 두 가지 방식으로 표현할 수 있다. 

 

아래 그림을 보면 최종적으로 끝마디가 결정된 후 그 안의 값들의 평균을 예측값으로 가진다. 

 

뒤에 다시 언급하겠지만 평균이 가장 간단하면서 성능이 잘 나온다. 

위의 결정 과정을 함수로 표현하면 아래와 같다. 

c는 끝노드 R에서 예측한 예측값을 뜻한다. 

 

I는 indicator function으로 중괄호의 조건이 참일 때 1, 거짓일 때 0을 반환하는 함수이다. 

 

즉, 위의 식을 정리하자면 해당하는 끝노드의 예측값만 남게되는 것이다. 

 

## 비용함수 (cost function)

위의 예제를 일반화하면 아래와 같다. 

 

m은 끝마디의 수를 뜻한다. 

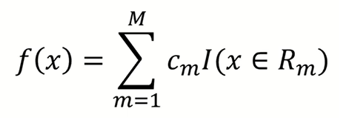
최상의 분할은 비용함수를 최소로 할 때인데 비용함수는 아래와 같다. 

위 함수를 최소화 하기 위한 c를 찾는 것이 중요한데 결론은 평균일 때 오류가 최소가 된다. 

 

(평균이 왜 가장 좋은지 유도하는 과정은 생략)

 

## 분할변수(j)와 분할점(s)

비용함수 다음으로 생각해봐야할 것이 두 가지 있다. 

① 어떤 변수를 사용할 것인가?

② 어떤 지점에서 분할할 것인가?

 

예를 들어 x₁ = {2, 3, 5, 6, 7}인데 3을 기점으로 분할했다면 j는 1이고 s는 3이다. 

 

분할변수 j와 분할점 s에 따라 끝노드 R이 결정되므로 j와 s를 구하는 것이 중요하다. 

j, s를 구하는 방식은 수식으로 표현하면 아래와 같다. 

 

argmin은 수식을 최소로 하는 j와 s를 구한다는 뜻이다. 

수식을 이해하기 위해 예시를 살펴보면

x₁={2, 3}, x₂={5, 6}, x₃={1, 7}이라 가정했을 때

j={1, 2, 3}, s={2, 3, 5, 6, 1, 7}이 될 것이고 모든 조합에 대한 cost를 구해본다. 

 

만약 (j, s) = (2, 5)에서 비용함수가 최소라면  x₂ >= 5, x₂ < 5 두 영역으로 분할하게 된다. 

 

# 분류나무 모델 (Classification Tree)

비슷한 범주끼리 모여있도록 하는게 목적이며 표현 방법은 예측나무 모델과 유사하다. 

 

다만 분류니까 값이 아닌 범주를 예측한다.

수식을 살펴보면 일단 몇 가지 기호를 알아야 한다. 

 

p hat m k는 끝노드 m에서 k클래스에 속한 관측치의 비율을 뜻한다. 

 

예를들어 1번 끝노드의 5개의 관측치 중 1이 3개라면 p₁₁ hat은 0.6이다. 

 

N은 관측치의 개수를 뜻하며 R은 끝노드를 뜻한다. 

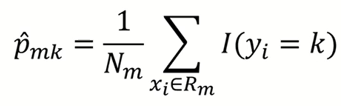
k(m)은 끝노드 m으로 분류된 관측치가 어떤 클래스로 분류되냐를 뜻한다. 

 

확률 p가 가장 큰 경우의 k로 분류된다. (argmax)

분류 알고리즘을 수식으로 표현하면 아래와 같다. 

I는 역시 indicator function이므로 결국 해당하는 끝노드의 k만 남게된다. 

 

## 비용함수

분류 모델에서 비용 함수 여러 종류가 있다. 

참고로 각 함수별로 분포가 조금씩 다르다. 

(cross-entropy의 경우 p=0.5일 때 값이 1인데 아래 그래프에서는 스케일링 되어있다. )

아래와 같은 예시로 오분류율(misclassification rate)를 구해보면 다음과 같다. 

L은 대다수가 0이니 1이 오분류고, 오분류율은 21 / (63 + 21) = 0.25

R은 대다수가 1이니 0이 오분류고, 오분류율은 37 / (37 + 79) = 0.32

 

총 오분류율은 (37/116) * (116/200) + (21/84) * (84*200) = 0.29 이다. (왼쪽이 R, 오른쪽이 L)

 

아래와 같은 다른 예시로 Gini 계수와 Entropy를 구해보면

Gini 계수는 (6/7 * 1/7) + (1/7 * 6/7) = 0.2449

Entropy는 -(6/7)log(6/7) - (1/7)log(1/7) = 0.1781

 

참고 - Information Gain

특정 변수를 사용했을 때의 entropy 감소량으로 아래와 같이 계산할 수 있다. 

 

아래 식에서 S는 전체 크기를 뜻하며, v는 변수 A의 값인데 |Sv|는 각각의 v에 대한 크기를 뜻한다. 

entropy를 크게 감소시켰다면 해당 변수는 중요하다고 생각할 수 있다. 

 

## 분할변수(j)와 분할점(s)

예측모델과 마찬가지로 아래 두 가지를 생각해야한다. 

① 어떤 변수를 사용할 것인가?

② 어떤 지점에서 분할할 것인가?

 

결론적으로 나눌 때 마다 불순도가 낮아져야 하며 비용함수가 최소가 되어야 한다. 

 

예시로 클래스 0과 1의 비율이 45%, 55%인 노드는 90%, 10%인 노드에 비해 순수도가 낮다. 

 

불순도가 높다고도 표현이 가능하며 같은 값끼리 모여 있을수록 더 순수하다고 볼 수 있다. 

 

j와 s를 찾는 것을 수식으로 표현해보면 아래와 같다. 

 

아래는 cost function으로 Misclassification rate를 사용한 것이며 대괄호 안의 식이 이에 해당한다. 

 

# 개별 트리 모델의 단점

계층적 구조이므로 에러가 중간에 발생하면 다음 가지로 에러가 계속 전파된다. 

 

학습 데이터의 미세한 변동에도 나무 자체가 크게 바뀔 수 있어서 최종 결과 또한 영향을 받을 수 있다. 

 

노이즈에도 영향을 많이 받는다. 

 

그리고 끝마디 갯수를 너무 늘리면 과적합 위험이 있다. 

 

다음에 정리하겠지만 이런 단점을 해결하는 모델이 랜덤 포레스트이다. 

 

 

참고 : 김성범 교수님 유튜브