로지스틱 회귀모델(Logistic Regression)

# 개요

예측하려는 값이 범주형일 경우 선형회귀를 사용하기 어렵다. 

가령 위와 같은 데이터를 점으로 찍으면 아래와 같을텐데 선형으로 적합하기는 어렵다. 

 

이럴 경우 아래와 같이 그룹별로 묶어서 확률을 구하면 아래와 같다. 

확률로 접근하면 선형회귀로 접근할 수 있게 되는데

확률이므로 0에서 1의 값을 가지는 아래와 같은 시그모이드 함수가 더 적합하다. 

 

범주 예측은 이런 식으로 로지스틱 회귀모델을 사용할 수 있다. 

 

# 로지스틱 함수

로지스틱 함수는 아래와 같다. 

 

특징으로는 x는 -∞에서 ∞값을 가지지만

y값은 무조건 0에서 1사이의 값이 나온다. 

다른 특징으로 로지스틱 함수를 미분하면 로지스틱 함수의 곱으로 표현된다는 것이다. 

이 특징은 추후에 Gradient learning method에 유용하게 사용된다. 

 

π는 x값이 주어졌을 때 y가 1이 될 확률을 뜻하며 y의 기댓값이라고도 한다. 

즉, 1에서 y가 0이 될 확률을 빼는 것과 같다. 

 

이와 같이 입력변수 x가 1개인 것을 단순로지스틱 회귀모델이라 부르며 아래와 같다. 

식을 보면 선형 함수식이 지수에 들어가 있다. 

 

선형회귀때는 이 β를 통해 x값이 증가하면 y가 얼마나 증가하는지를 알 수 있었다. 

그러나 이런 비선형에서는 해석이 직관적이지 않다. 

 

그래서 승산(Odds)라는 개념이 나온다. 

 

# 승산 (Odds)

 성공 확률을 p로 정의했을 때, 실패 대비 성공 확률의 비율을 뜻한다. 

p = 1 이면 odd = ∞

p = 0 이면 odd = 0

 

승산은 보통 도박에서 배당금에 많이 쓰인다. 

 

2018 월드컵 도박을 보면 독일 우승에 돈을 걸면 4배를 받을 수 있다. 

한국 우승에 돈을 걸면 500배를 받을 수 있다. (이해가 팍팍)

즉 승산으로 우승 확률을 계산해 볼 수 있다. 

프랑스의 승:패 비율은 11:2이고 odds는 2/11이다. 

프랑스의 우승 확률은 2/13=0.15(15%) 가 된다. 

 

다시 로지스틱회귀의 승산으로 돌아가보면 π는 확률을 뜻한다. 

그리고 Odds는 아래와 같은데 분자는 범주 1일 확률, 분모는 범주 0일 확률을 뜻한다. 

여기서 중요한건 Odds에 로그를 씌우면 선형 결합 형태로 바뀐다는 것이다. (Logit Transform)

즉 β1에 따라 x가 증가할 때 log(Odds)가 얼마나 증가하는지 설명할 수 있으므로 해석이 더 쉬워졌다. 

 

# 파라미터 추정

파라미터 추정이란 β값을 찾는 것을 의미한다. 

 

## log likelihood function

로지스틱 회귀에서는 y는 0 또는 1이 나타나므로 베르누이 분포를 따른다. 

이 때 likelihood 함수는 곱으로 나타낼 수 있다. 

곱보다는 더하기가 계산이 편하므로 로그를 씌우고 정리하면 아래와 같이 log likelihood 함수가 나온다. 

 

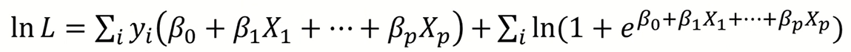
## Maximum Likelihood Estimation

우리는 위의 log likelihood function이 최대가 되는 파라미터 β를 찾아야 한다. 

 

문제는 파라미터 β에 대해 비선형이므로 명시적인 해가 존재하지 않는다. (No closed-form solution exists)

 

그래서 수치최적화 알고리즘을 사용해서 해를 구한다. 

 

## Cross entropy

log likelihood function을 최대화 하는 파라미터를 찾는다는 말은

cross entropy를 최소화한다는 것과 같은 의미이다. 

 

log likelihood function을 최대화 하는 것 보다 풀기가 쉽나보다. 

왜인지는 설명을 안해주시니 일단 패스

 

 

# 결과 및 해석

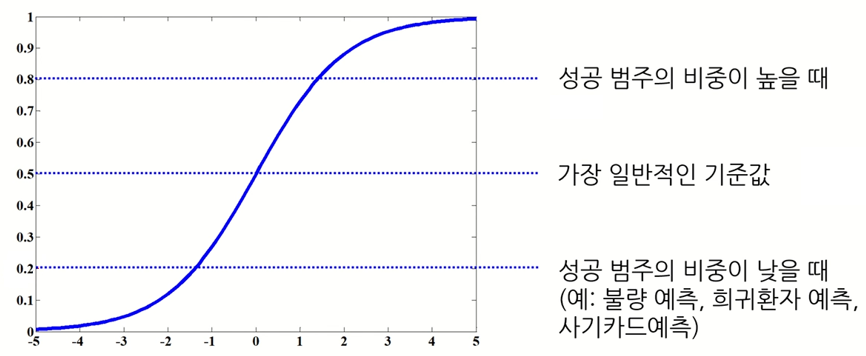
로지스틱 회귀함수는 결국 확률값을 주기 때문에 이진 분류를 위해서는 threshold가 필요하다. 

 

일반적으로는 0.5를 쓰는데 도메인의 특성에 따라 다르다. 

 

## 승산 비율 (Ordds Ratio)

선형회귀모델에서는 β가 입력변수가 1 증가할 때 출력변수가 얼마나 증가하는지를 뜻한다. 

 

로지스틱회귀에서는 이와 달리 위에서 정리했듯 log(Odds)의 변화량을 뜻한다. 

 

이걸 이용해서 승산 비율 (Odds Ratio)라는 것을 구할 수 있는데 아래와 같이 정리된다. 

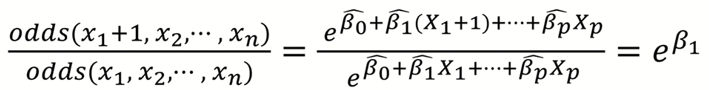
승산 비율의 정의는 아래와 같다. 

"나머지 입력변수는 모두 고정시킨 상태에서 한 변수를 1단위 증가시켰을 때

변화하는 Odds(성공확률)의 비율"

 

 

즉 쉽게 설명하면 x₁이 1 증가할 때 마다 승산 비율이 e^(β₁) 만큼 변한다는 뜻이다. 

회귀 계수(β hat)가 양수 → 성공 확률 증가 

회귀 계수(β hat)가 음수 → 성공 확률 감소

 

# 예제

대출 여부를 예측하는 데이터로 로지스틱 회귀모델을 만들었다고 가정하자. 

결과는 아래와 같이 나왔다. 

Coefficient

해당 변수가 1 증가했을 때 log(Odds)의 변화량을 뜻한다. 

양수면 성공 확률과 양의 상관관계, 음수면 음의 상관관계를 가진다. 

 

Std.Error

추정 파라미터의 신뢰구간(구간추정)을 할 때 사용한다. 

 

p-value

해당 변수가 통계적으로 유의미한지 알려준다. 

 

Odds

여기서는 Odds Ratio를 뜻한다. 

 

예시로 Experience에 대한 Odds Ratio가 1.058이므로

"경험이 1년 더 많으면 대출 확률이 1.058배 증가한다." 라고 해석할 수 있다. 

 

# 정리

로지스틱 회귀함수는 선형회귀함수와는 달리 범주형 데이터 예측에 사용된다. 

 

비선형이므로 해석이 쉽지 않아서 승산(Odds)라는 개념을 사용한다. 

 

또한 비선형이므로 미분을 통해 최적의 파라미터를 찾을 수 없다. 

 

그래서 Log Likelihood Function을 최대화하거나 Cross Entropy를 최소화하는 방식으로 파라미터를 찾는다. 

 

결과는 이진 분류를 위해 threshold가 필요하다. 

 

해석은 Odds Ratio를 통해 해당 파라미터가 얼만큼의 영향을 미치는지 알 수 있다. 

 

 

 

참고 : 김성범 교수님 유튜브