카이제곱분포, t분포, F분포

# 카이제곱분포

카이제곱분포는 짧게 대략 표현하면 표준정규분포 제곱의 합의 분포라고 볼 수 있다. 

 

카이제곱분포에서는 각각의 확률변수는 아래와 같이 표준정규분포를 따른다고 가정한다. 

이 때 각각의 확률변수를 제곱해서 더한 새로운 확률변수 Z는 카이제곱분포를 따른다. 

여기서 v는 자유도라고 부르는데 표준정규분포를 몇 개 더했는지를 뜻한다. 

밀도 함수는 아래와 같이 생겼다. 당연히 외울 필요는 없다. 

평균은 v, 분산은 2v이다. 

카이제곱분포는 감마분포에서 α=v/2, λ=2인 스페셜 케이스에 해당한다. 

 

## 자유도

자유도에 대해서는 쉽고 명확하게 설명해주는 책은 없다. 

 

좀 쉽게 컨셉을 설명해보자면

만약 x1, x2, x3, x4, x5의 합이 20으로 이미 정해져있다면,

x1, x2, x3, x4를 정하는 순간 x5는 자동으로 결정된다. 

즉 평균의 경우 자유도가 n-1이 된다. 

 

표본 분산의 자유도가 n-1인 것도 위와 같은 이유로 보면 된다. 

 

# t 분포

Z가 정규 분포를 따르고 Y가 카이제곱분포를 따른다고 했을 때

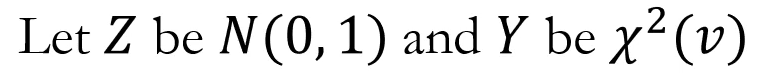
t분포는 아래와 같이 정규 분포와 카이제곱분포의 조합으로 이루어져있다. 

카이제곱분포의 자유도는 t분포로 그대로 이전된다. 

 

t분포의 기댓값은 0이고 대칭형이며 표준정규분포보다는 꼬리가 더 길다. 

 

t분포든 카이제곱분포든 모두 모집단은 정규분포를 따르는 것을 가정하고 있다. 

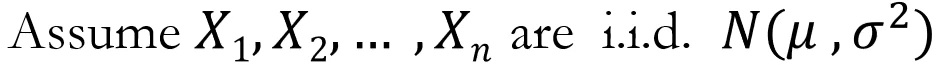
그리고 Z와 Y는 각각 아래와 같이 표현할 수 있다. 

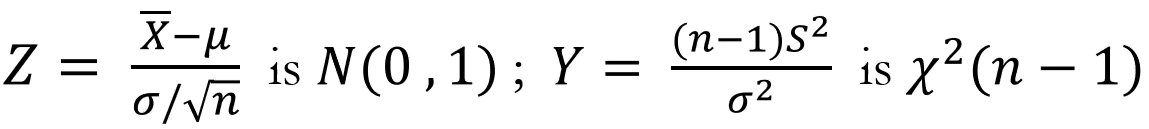
t분포의 정의에 따라 대입해서 정리하면 아래와 같이 된다. 

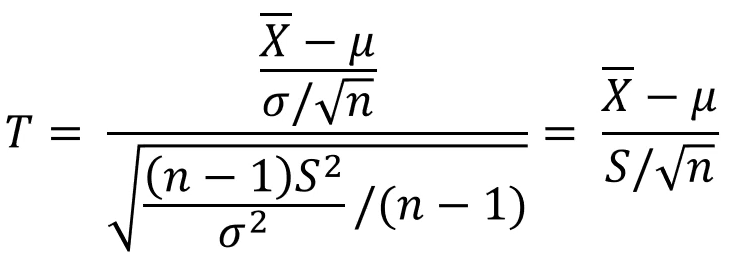
정리된 꼴을 보면 표준정규분포와 같은데 모표준편차 대신 표본표준편차가 쓰였다. 

 

즉, 모집단의 표준편차를 알면 표준정규분포를 사용할 수 있고,

모집단의 표준편차를 모르면 표본 표준편차를 가지고 t분포를 사용한다. 

 

 

# F 분포

카이제곱분포를 따르는 확률변수 Y1, Y2가 있을 때

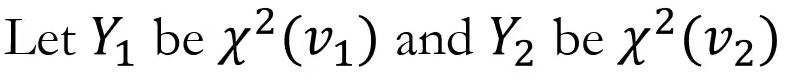
F는 다음과 같이 정의된다. 

표기는 F(v₁, v₂) 이런 식으로 자유도로 표기한다. 

F분포를 말할때는 꼭 자유도를 같이 말해야한다. 

 

계산을 하다보면 α대신 1-α에 대한 값을 구하게 되는 때가 있는데

아래와 같이 역수가 되면서 자유도 v₁, v₂의 위치가 바뀜에 주의하자. 

F분포는 아래와 같이 skew된 그래프이고 자유도에 따라 달라진다. 

 

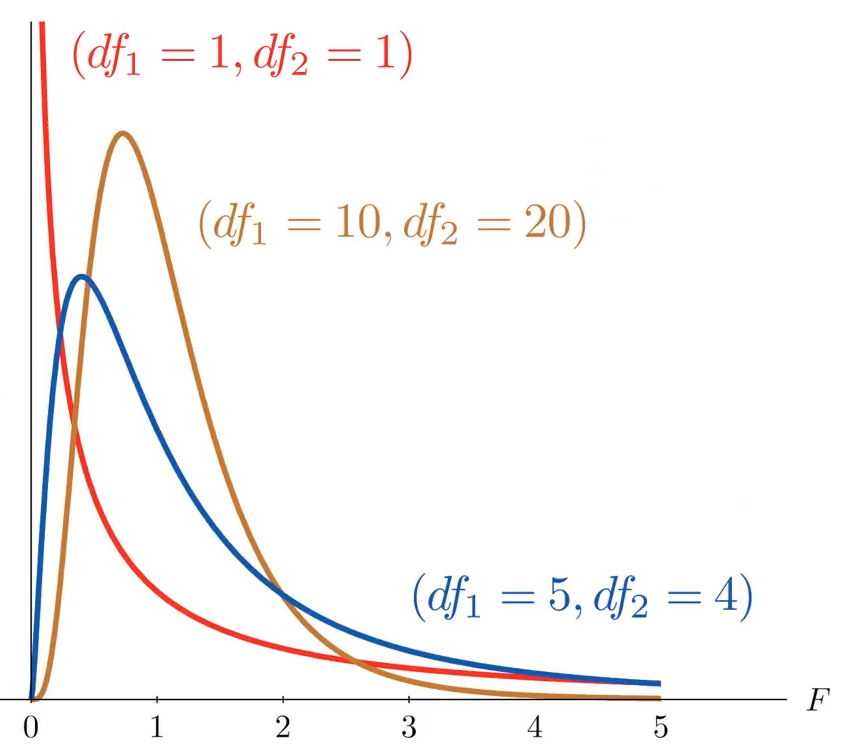
아래와 같은 두 모집단으로부터 각각 표본을 뽑았다고 가정해보자. 

F분포의 정의에 따라 식을 전개하면 아래와 같다. 

위 식은  F(n₁-1, n₂-1)과 같이 표현할 수 있다. 

 

## 예시

이 전개를 기억하고 예시를 살펴보면

 

아래와 같이 모집단의 평균과 분산이 알려져 있을 때

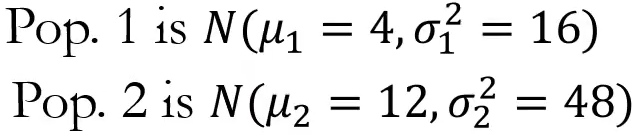
아래의 모분산과 표본분산으로 이루어진 값은 F분포를 따른다. 

아래와 같은 조건을 만족하는 c값을 구한다면 

모집단의 분산은 이미 알려져있으니 아래와 같이 전개해서 c값을 구할 수 있다. (f값 찾는건 생략)