표본 분포(Sampling Distribution)

# 모집단과 표본

population : 모집단 (전체)

sample : 모집단의 일부

통계 : 표본을 이요하여 모집단의 특성을 파악하는 학문

 

모집단, 표본의 평균과 분산은 아래와 같은 기호를 쓴다. 

 

# 통계량

통계학에서 가장 중요한 세 개의 함수는 아래와 같다. 

① 확률 변수  ②확률 함수  ③ 통계량

 

크기가 n인 샘플을 뽑았을 때 이 샘플들에 대한 함수를 통계량이라고 부른다. 

 

 

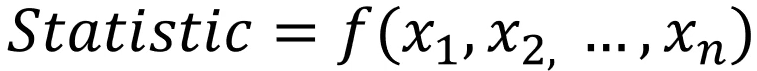
아래와 같이 표본 평균, 표본 분산이 대표적인 통계량이다. 

 

# 표본 분포 (Sampling Distribution)

통계량의 분포를 뜻한다. (표본 평균, 표본 분산)

 

모집단의 분포를 N(μ, σ²)라 가정하고 각각의 샘플들도 같은 분포로 뽑았다면 

(i.i.d. : independent identically distributed)

## 표본 평균의 분포

표본 평균의 분포는 아래와 같은 정규 분포를 따른다.  

(표본의 분포가 아니라 표본 평균의 분포이다. 처음 배울때는 이게 헷갈렸음..)

이게.. 용어가 좀 헷갈릴 수 있는데 정리해보면

• 모집단의 평균은 μ (가정)
• 표본의 평균도 μ (가정)
• 표본 평균의 평균도 μ (표본 평균의 분포, 중심 극한의 정리)

 

아래와 같이 표준 정규 분포로도 바꿀 수 있다. 

위와 같은 조건의 두 개의 모집단에 대해 살펴보면 표본 평균

 

## 표본 분산의 분포

표본 분산은 조금 복잡한데 S²의 분포는 바로 정의할 수가 없다. 

 

아래와 같이 표현할 수 있는데,

n-1과 σ²는 상수이므로 표본 분산이 카이제곱 분포를 따른다고 해도 된다. 

 

 

# 중심 극한 정리 (Central Limit Theorem)

모집단이 정규 분포를 따를 때는 아래와 같이 표본 평균이 다음 분포를 따른다.  

하지만 중심 극한 정리에 따르면 굳이 모집단이 정규 분포가 아니라도 

 

표본의 크기가 충분히 크다면 모집단의 분포와 상관없이 표본의 평균은 정규 분포를 따른다. 

(충분히 크다 : n ≥ 30)

 

교과서적으로 정리하면 아래와 같다.